It seems unnecessary, even silly to say it, but basketball is a very simple game. Ever since the late 1930s when the college rules committee eliminated the mandatory center jump after every score, the game became one of transition, the competitors converting from offense to defense and back again in near seamless fashion.
Essentially the game requires you to trade possessions and attempt to score when it’s your turn. You win by outscoring your opponent as the possessions unfold, one after another. It’s a possession-by-possession game.
Modern analytics and the effort to determine how best to measure a team’s performance finds its origins this understanding.
Like many insights, a number of people likely came to the same conclusion in different places, under different circumstances, so it’s hard to say who gets credit or took the first steps. But conventional wisdom cites the work of a young Air Force Academy assistant who questioned the accuracy of using traditional stats like points per game to measure a team’s offensive and defensive efficiency.
Dean Smith had majored in mathematics at Kansas while playing for the legendary Phog Allen and claimed he would have been happy to have become a high school math teacher, but in 1955 head coach Bob Spear offered him a job at the newly opened Academy.
In his role as Spear’s assistant, Smith began to probe the possession-by-possession nature of the game and reasoned that a game’s tempo or the pace of play skewed statistical conclusions because teams played at different speeds.
“I have never felt it was possible to illustrate how well we were doing offensively based on the number of points we scored. The tempo of the game could limit us to fifty points and yet we could be playing great offense. In some games we might score eighty-five points and yet be playing poorly from an offensive viewpoint… From a defensive point of view, one of my pet peeves is to hear a team referred to as the ‘defensive champion’ strictly on the basis of giving up the fewest points per game over a season. Generally, a low-scoring game is attributable to a ball control offense rather than a sound, successful defense.”
To Smith, the only way to remove the bias of tempo was to accurately count each team’s possessions and ask “who made the most of the possessions they had?” By calculating how many points a team scored and allowed per possession, one could gain a clearer picture of how “efficient” a team had performed and compare it with other teams no matter whether they favored a slow tempo or a fast one.
To that end, Smith devised a statistical tool he called “possession evaluation” and began measuring the Academy performance through its prism. Four years later, in 1959, while serving as an assistant for Frank McGuire at North Carolina, Smith described the system in McGuire’s book, Defensive Basketball.
“Possession evaluation is determined by the average number of points scored in each possession of the ball by a team during the game. A perfect game from an offensive viewpoint would be an average of 2.00 points for each possession. The defensive game would result in holding the opponent to 0.00 (scoreless). How well we do offensively is determined by how closely we approach 2.00 points per possession. How close we come to holding the opponent to 0.00 points per possession (as opposed to holding down the opponent’s total score) determines the effectiveness of our defensive efforts. Our goals are to exceed .85 points per possession on offense and keep our opponents below .75 point per possession through our defensive efforts.”
Four decades later, Smith’s pioneering work found its way into Dean Oliver’s 2004 breakthrough book on statistical analysis, Basketball on Paper, in which he outlined his now famous “four factors” of basketball efficiency.
Oliver took the three broad statistical categories we’ve always used to measure performance – shooting, rebounding, and turnovers – added some nuance by including free throws and offensive rebounds to his equations, calculated the per possession value of each, and then multiplied the resulting percentages by 100 to determine a team’s offensive and defensive efficiency ratings. For Oliver, a team that had a higher offensive rating (points scored per 100 possessions) than its defensive rating (points allowed per 100 possessions) was more efficient than an opponent with lower ratings and the likely winner of a game between the two.
Combined with the onslaught of the three-pointer and its dramatic impact on coaching strategy, advanced analytics became a mainstay in sports journalism. You would be hard pressed to watch a game on television today or to read an account of it tomorrow without hearing references to one or more of Oliver’s descendants in the field – Ken Pomeroy, Kirk Goldsberry, Seth Partnow, Jordan Sperber, or Jeff Haley, to name a few.
And it makes good sense. The data is fascinating and often insightful.
• Team A plays fast, averaging 85 points per game but from an efficiency perspective, barely a point per possession while its upcoming opponent, Team B, averages 1.2 points per trip down the floor. Can Team A force Team B into a running game in hopes of disrupting Team B’s preferred rhythm and offensive efficiency? Or might an adjustment in Team A’s defensive tactics push Team B deeper into the shot clock where the data reveals that their shooting percentage drops?
• In its last game, our opponent, Team C, had an excellent offensive efficiency rating of 1.20, averaging 79 points on 66 possessions, but turned the ball over 16 times. In the 50 possessions when they protected the ball, their efficiency rating jumped to 1.58. What can they do to cut down on turnovers in the season ahead and grow more efficient?
• Team D is a weak shooting team but a high volume of their shots are 3-point attempts. They make enough of them to offset their misses and keep the score tight. What can we do to either reduce the number of 3-pointers they take or further erode their shooting percentage?
But there’s a problem.
While data comparisons can be purified by eliminating tempo mathematically, the game itself is not tempo-free.
Not tempo or pace narrowly defined as the number of possessions a team experiences in the course of a game, but the rate of speed or intensity at which things takes place during those possessions… or perhaps more precisely, the speed and intensity of a team’s actions relative to the speed and intensity of its opponents’ actions.
What do the military boy say? Speed kills?
In this sense, tempo is a weapon as speed or intensity, or a combination of the two, can shatter an opponent’s cohesion, throw them off balance, confuse and disrupt their preferred rhythm, challenge their confidence. It often creates fatigue and doubt. For example, determined and aggressive offensive rebounding not only creates more scoring opportunities, it disheartens defenders who have worked hard to prevent easy shots, only to see their opponent get the ball back for another try.
Basketball is filled with sweat and blood, and wild swings of emotion. Games run the gamut from stupid, unforced errors, missed shots, confusion and fatigue to gut-wrenching, scrambling defensive stands and exhilarating, fast-paced scoring runs … and moments of just plain luck. In combination, these can lead to what coaches call “game slippage” – a growing dread that your lead is slipping away and there is nothing you can do to stop it.
It’s impossible for data, tempo-free or not, to fully capture or quantify such realities.
In his recent book, The Midrange Theory, NBA analyst Seth Partnow eloquently acknowledges this fact, citing the foundational principle of general semantics first outlined by linguist S.I. Hayakawa in 1939: The map is not the territory… the word is not the thing.
A word or a symbol or a mathematical equation or even a lengthy written description is only a representation of reality… it’s never the reality itself, just as a map is not the territory it attempts to depict. No matter how nuanced and precise it becomes, advanced analytics can never capture the totality of the decisions, actions, and outcomes that comprise a basketball game.
Today’s advanced, computer-generated analytics often miss the context, the circumstances, the “how and why” of what takes place on the court.
The stats of the 1963 NCAA championship game between Loyola and Cincinnati that we introduced in our last post don’t explain why – after shooting 73% on 8 of 11 shots in the opening minutes of the second half – Cincy’s Ron Bonham and his teammates took only 3 more shots in the remaining 13 minutes of regulation and blew a 15-point lead.
Nor do they explain how and why Bonham’s All-American counterpart on Loyola, senior captain Jerry Harkness, failed to make a single basket in the first 35 minutes of play, but then exploded. With 4:34 left in regulation, he scored his first field goal, followed ten seconds later by a steal and a second basket. At the 2:45 mark Harkness scored a third basket and with only four seconds left on the clock, connected on a 12’ jumper to tie the game and send it to overtime. On the opening tip of the overtime period, he scored his fifth and final field goal.
In the course of 242 desperate seconds, Harkness scored 13 points on five field goals and three free throws, propelling Loyola to the national championship. His frenetic intensity on defense, coupled with mad dashes up the floor hoping to spark the Ramblers’ fast break, typified the Chicagoans’ up-tempo, less than efficient, but highly effective approach to the situation in which they found themselves.
Predictably, according to the conventions of advanced analytics, both teams had roughly the same number of possessions, 67 for Cincinnati, 69 for Loyola… an average of 68 apiece. As the game unfolded, they traded possessions, each taking their turn with the ball. But while this accounts for the relatively slow “mathematical” tempo or pace of the game, it masks the relative speed and intensity – the operational tempo – of what took place within those possessions.
For example, in less than a third of its possessions, Loyola generated 42 field goal attempts, nearly equaling Cincinnati’s total output for the entire game.
You won’t find those numbers revealed in the efficiency stats of the game.
Loyola was horribly inefficient but, in the end, effective because their rapid pace and intensity generated 30 more scoring opportunities: 77 field goal attempts to the Bearcats’ 47. Even in the overtime period, Loyola fired six more times than Cincy. They converted only 33% of them, half of Cincinnati’s 67% rate, but enough to give them one more basket as the clock expired.
The sheer volume or statistical raw count of Loyola’s attack confounds the tempo-free, efficiency percentages of the Four Factors.
Analytics picks up the underlying drivers – Loyola’s offensive rebounding and tenacious defense leading to Cincy turnovers turned the game around – but assigns values based on percentages that are misleading.
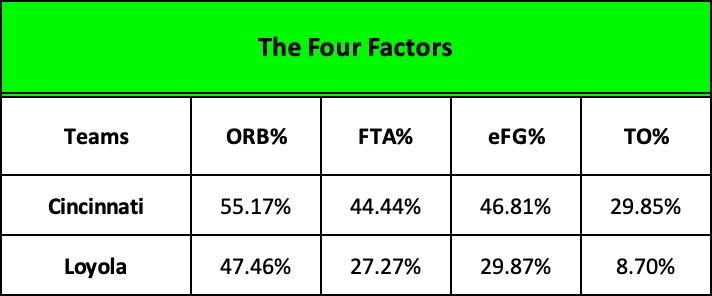
Let’s start with key indicator of efficiency and likely victory in the both the NBA and college ranks, the eFG% or “effective field goal shooting percentage.”
It’s calculated just like the traditional FG%: you divide a team’s “makes” by its “attempts” to determine its shooting percentage. For example, 20 baskets divided by 50 attempts yields a shooting percentage of 40%. But the modern efficiency calculation makes an important adjustment to the formula. Recognizing the impact of today’s 3-pointer, it grants 50% more credit for made 3-pointers. If 6 of those 20 baskets were 3-pointers, the efficiency calculation climbs from 40% to 46%. From an efficiency standpoint, it’s as if the team had made 23 two-point baskets instead of only 20.
Since there were no 3-pointers in 1963, the eFG% formula for Loyola and Cincinnati is no different than using the traditional version. Clearly, Loyola was horrendous, making only 30% of its 77 shots while Cincinnati scored a very respectful 47%. But, the sheer volume of Loyola’s attempts renders an efficiency comparison between the two meaningless.
Cincy’s first, last, and total 47 attempts yielded 22 baskets… while Loyola’s first 47 attempts yielded only 12, putting them 20 points behind. But the Ramblers went on to attempt an additional 30 field goals… and made 11 of them, winning the game by 2.
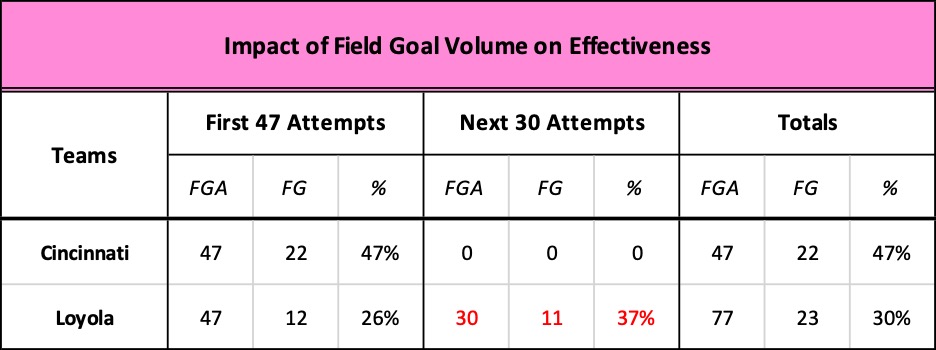
Comparing each team’s ORB% or offensive rebounding percentage leads to the same problem.
This measurement calculates the percent of offensive rebounds a team secures on its missed FG attempts. It’s an important indicator of offensive efficiency because an offensive rebound extends a possession, creating an opportunity for a second attempt to score more points.
Once again, Cincy achieved higher efficiency rating than Loyola, snagging 55% of their offensive rebound opportunities compared to Loyola’s 47%. But Cincy’s advantage in the comparison is the “mathematical” consequence of attempting 30 fewer field goals.
Loyola’s raw numbers tell us more about the actual pace, intensity, and outcome of play than the analytic scores do.
In just 24 of its possessions, Loyola grabbed 28 ORBs and generated 42 FGAs, nearly as many as Cincy attempted in the entire game. The Bearcats outperformed Loyola in the ORB% factor but produced 12 fewer scoring opportunities and 11 fewer points.
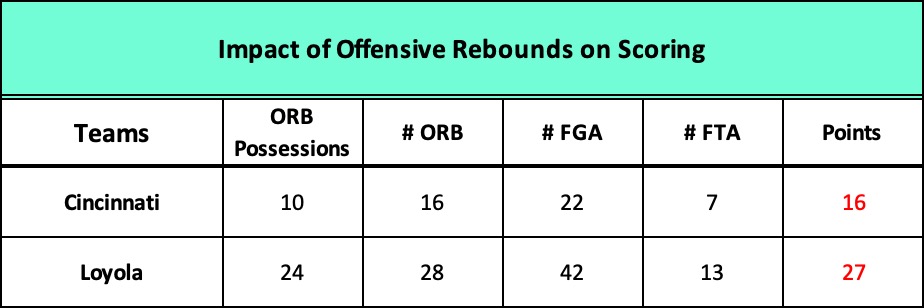
The efficiency factor called the FTA% captures a team’s ability generate free throws in proportion to the number of FGs it attempts. The idea is that free throws are statistically easy, highly efficient points to score because the shooter is unguarded, so a team with a higher FTA% than its opponent is likely the one that was more proficient in attacking the defense and getting to the line. In the modern game the FTA% is increasingly relied upon to measure how much pressure a team or specific scorers exert on the defense.
Once again, the wide disparity in the number of field goal attempts between Loyola and Cincinnati makes the comparison irrelevant. Both teams attempted the same number of free throws and made the same number, 14 for 21. Cincinnati’s higher rating had nothing to do with the outcome of the game.
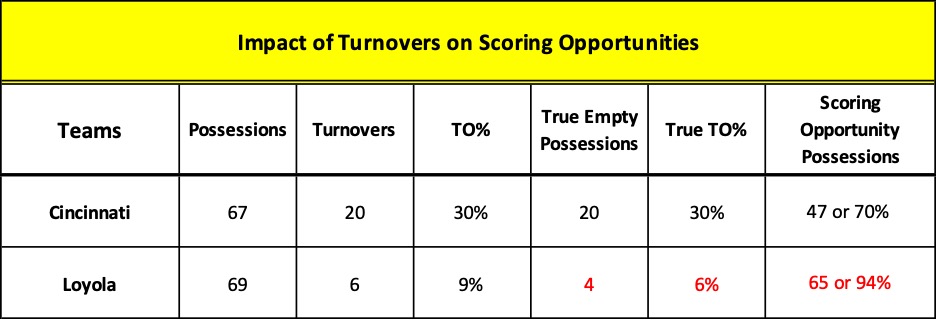
Next to shooting percentage, the most important indicator of offensive efficiency and likelihood of victory in the NBA and college ranks is the TO% or turnover rate. (On the high school level, many coaches believe that it is the most critical of the Four Factors.)
The TO% tells us how well a team protected the ball by determining the percentage of its possessions that resulted in a turnover. Its importance makes sense because if you lose the ball, you may end up with an “empty possession” – one in which you lost the opportunity to score.
In the Loyola – Cincinnati tilt, it is the only one of the Four Factors that demonstrates actual efficiency. Loyola turned the ball over 6 times in 69 possessions – 9% of the time – compared to Cincinnati’s horrendous 20 times or 30%. But the reality was even worse.
That’s because two of Loyola’s turnovers occurred during possessions in which they rebounded missed FGAs and then lost the ball. In other words, these possessions were not “empty” as they attempted a field goal and only lost the ball after securing the offensive rebound. In Cincinnati’s case, all twenty turnovers resulted in empty possessions.
Perhaps a clearer way to look at it is to compare the number of “true” or pure empty possessions. From this perspective, Loyola had chances to score in 94% of its possessions, not the 91% suggested by the TO% formula. Conversely, all twenty of Cincy’s turnovers resulted in an empty possession so they had chances to score in only 70% of their possessions.
The 1963 NCAA championship is a dramatic example of how advanced analytics often misses the significant impact of operational tempo on the outcome of a game.
Ironically, though Oliver and his fellow practitioners trace the origins of their work to Dean Smith’s “possession evaluation” in the 1950s, the underlying culprit may lie in how they departed from Smith’s definition of a possession and, more importantly, from his reasons for evaluating possessions in the first place.
Smith was interested in measuring his team’s efficiency regardless of the pace of the game. Comparing his team with his opponent did not require equalizing the number of each team’s possessions but looking, instead, at the per-possession performance of each team, given its particular pace or tempo. In other words, he didn’t strip tempo out of his calculations, he included it.
In Smith’s world, a possession ended and a new one began as soon as a team lost “uninterrupted control of the basketball.” Throw the ball out of bounds and your possession ended; shoot the ball and whether you made it or missed it, your possession ended. And if you regained control of a missed free throw or field goal with an offensive rebound, you started a new possession, a new opportunity to score.
In Oliver’s world, an offensive rebound continues the same possession. You don’t get credit for an additional one. That’s why by game’s end both teams will tally the same or close to the same number of possessions and why modern analytics can perform a “tempo-free” comparison of each team’s efficiency.
Smith wasn’t interested in making an exacting mathematical comparison of efficiency. Regardless of the game’s total number of possessions, whether the overall pace had been fast or slow, or whether one team had generated greater or fewer possessions than its opponent, he asked the same two questions: how many possessions or scoring opportunities did we create and how well did we perform in each of our possessions?
We know for certainty that Dean Smith was in Freedom Hall the night Loyola beat Cincinnati for the national championship. We don’t know if he charted the game and ran the results through his efficiency formula, but if he did, here’s what it would have looked like compared to the numbers using Oliver’s formula.
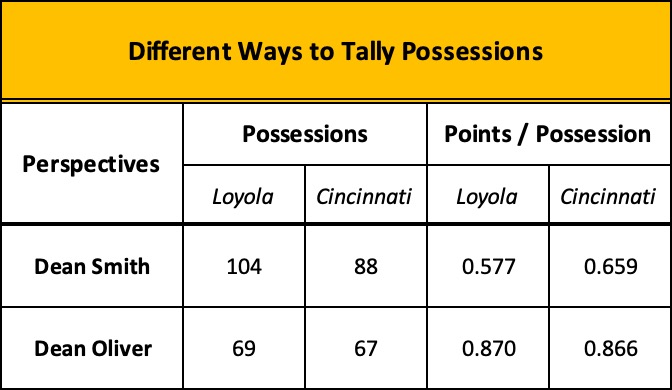
The end results are the same; do the multiplication and Loyola wins by two, 60-58… but Smith’s method of counting possessions paints a clearer picture of the operational tempo of the game.
Possession-by-possession, Loyola’s performance was woeful but in Smith’s view, they played at a faster pace, generating sixteen more possessions than Cincinnati. Couple Smith’s numbers with the game’s traditional stats and you get quick confirmation of what the average fan saw in the arena or on television that night: Loyola played terrible but shot more often, grabbed lots of rebounds when they missed leading to more shots, and rarely turned the ball over. They created more chances to score than Cincinnati did.
Smith’s method reminds us that pace or tempo as always been defined by the number of possessions but his simpler method of calculation – adding a team’s shot attempts, turnovers, and specific kinds of free throw attempts – comes closer to exposing the all-important but missing element of pace in today’s analytics – the passage of time. Consider the following:
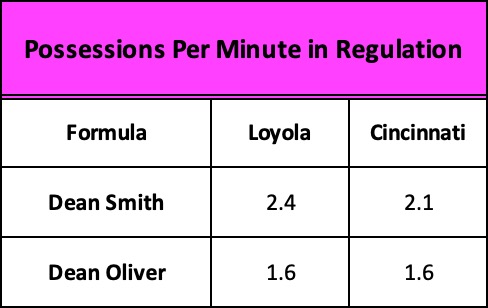
Whose count gets us closer to the actual pace of the game?
In 40 minutes of regulation play, Smith credits Loyola with 94 possessions to Cincy’s 83. Basically, every two minutes that passed off the game clock saw Loyola producing five scoring opportunities to Cincinnati’s four. When regulation time finally expired, the Ramblers had accumulated 11 more possessions and tied the game, pushing it into overtime.
Not only does Smith’s 70-year-old method more accurately reveal the game’s true speed and intensity, it suggests that the proverbial eye test is alive and well, and not easily dismissed by technology, algorithms, and today’s mathematical whiz kids – a theory we’ll explore in our next post.
But… before we go, one more irony to explore, this one pleasantly surprising.
Two nights before the 1963 NCAA championship game, George Ireland was preparing for his semi-final game against Duke, the ACC champs, when he was interrupted by a knock on his hotel room door. Standing outside was North Carolina’s young assistant who handed him a gift from UNC’s head coach, the legendary Frank McGuire. It was UNC’s scouting report on Duke who had defeated the Tar Heels to secure its bid to the NCAA tournament.
The young assistant? Dean Smith.

